“Space is big. You just won't believe how vastly, hugely, mind-bogglingly big it is. I mean, you may think it's a long way down the road to the chemist's, but that's just peanuts to space.”

Say you're in a simulation, and you want to throw a ball. Easy enough, you take what you know about classical mechanics and impart some force to your ball to give it an initial velocity. Then you take little steps forward in time, applying some force due to gravity at every one. You consider applying forces from air resistance too, but then remember you're a physicist, and think better of it.

Next, as you're in a simulation, you want to have some fun. You decide to throw it a bit harder - let's put this thing into orbit! You add a few zeroes to your initial throw and throw it straight ahead. To your dismay once the ball gets more than a few kilometres away it starts misbehaving. It stops moving smoothly and instead begins to jitter. Before long it's a complete mess, jumping from place to place and not really looking like it's been thrown at all.

Digging into your simulation, you find you've been using single-precision floating points. A rookie mistake! You change them all to double-precision, and throw again. This time, the ball sails smoothly away, and you watch it disappear over the virtual horizon. Satisfied, you pivot on the spot to await the ball's return. You estimate it should take 90 minutes or so, but dinner is in an hour, so you decide to hurry up and wait by speeding up time by a factor of a hundred.

At this rate, the ball will only be gone for a few seconds. You take these few seconds to recollect what you know about objects in orbit. Accelerating only due to the force of gravity, such objects move along elliptical trajectories. Every orbit, they pass through the same points, and every orbit, they take the same amount of time to do so. Checking your watch, you predict to the second when the ball will arrive, and slow things back to normal just in time to watch the ball appear in the distance. You hold your hand out in exactly the position you released the ball, since that position is on its orbit. You smile smugly, proud of your creation, and are just thinking of dinner when the ball arrives, hitting you squarely in the face.

It is straightforward enough to implement an n-body simulation of gravity based on Newton's law of gravitation. Unfortunately, physics calculations in games are done with floating-point arithmetic, of which a limitation is that numbers may only be approximately represented. Besides scale, a limited precision presents a subtle and hard to solve problem which is present in any iterative algorithm, such as an n-body simulation based on universal gravitation. As part of its operation, the state at the end of one discrete frame forms some or all of the input for the next. Due to the missing precision, error accumulates over time, resulting in larger discrepancies from reality the longer the simulation is run for.

Floating points are a fact of life in game physics, and we are not going to escape them here. So how does Kerbal Space Program do it?

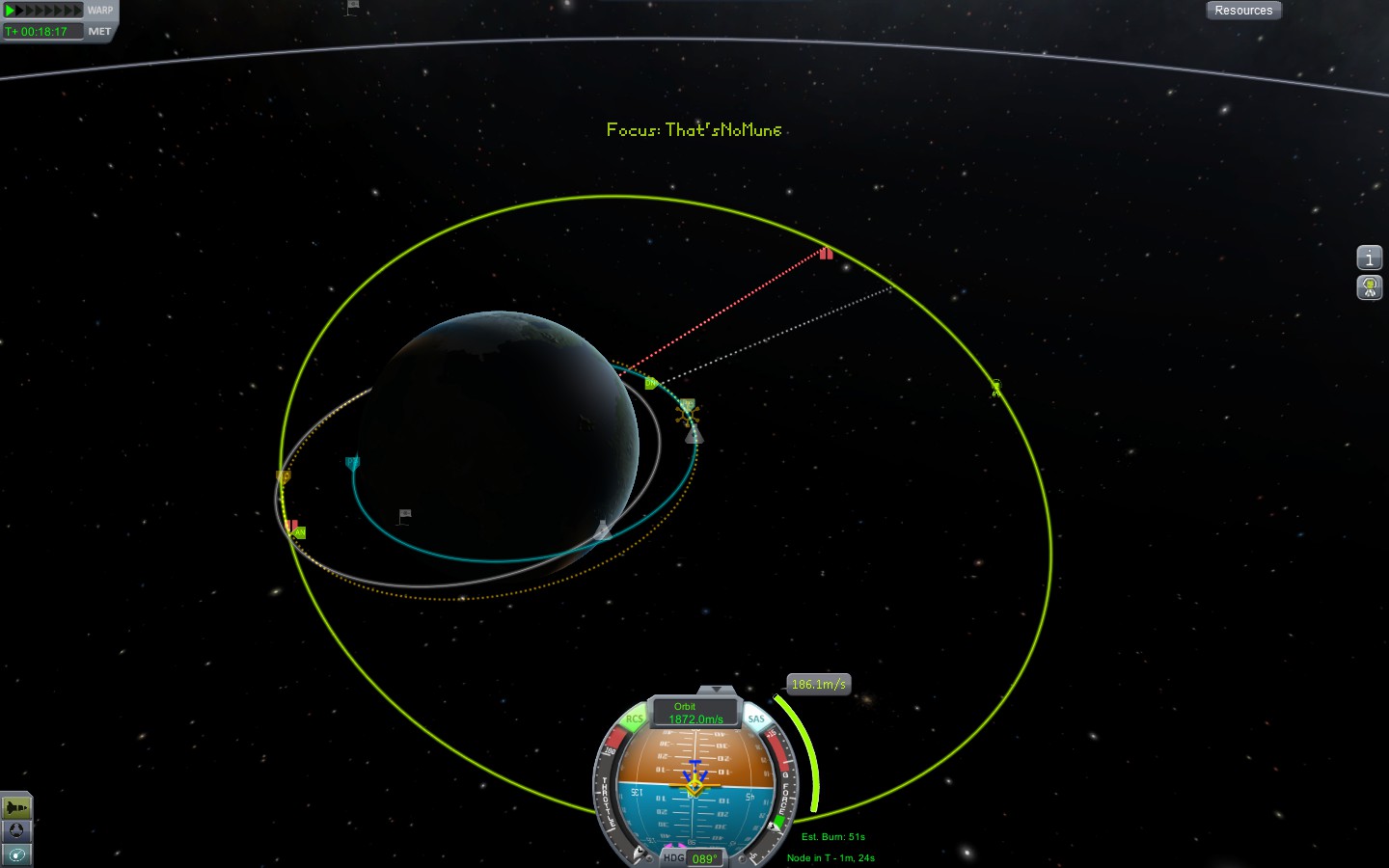
Kepler's laws make a simplification known as the two-body problem. Kepler's laws of planetary motion describe the elliptical path of a object in a stable orbit. This includes the paths of objects like the Moon and the International Space Station around the Earth, or the path of the Earth around the Sun. More complex systems, such as Sun-Earth-Moon or the entire Solar System can be modelled as a composition of several two-body systems, rather than the n-body systems they really are. This conveniently sidesteps the requirement to use approximate forces and therefore the accumulation of error over time. The two body problem describes the motion of one body around another, or more precisely a common barycentre. In the case of one massive and one tiny object, the barycentre is approximately in the same position as the centre of the larger object and can therefore be ignored. In a two-body system, an orbit is perfectly stable and cyclical. A body's position can thus be calculated directly as a function of time.

The ability to calculate positions directly as a function of time has some extremely valuable properties. One of the many challenges faced in deep space exploration is the sheer duration required by such voyages - the Voyager probes were launched nearly half a century ago, and even reaching Mars takes the better part of a year. To be of any real use, then, interactive astrodynamic simulations need a level of time control. Kerbal Space Program has a time warp feature, allowing players to navigate missions taking years of simulated time in an evening of real time.

This would not be possible with an iterative physics simulation, as the accuracy of the result is directly dependent on the resolution of the time step. Games have to produce several frames per second to both sell the illusion of motion and stay responsive, meaning each frame must be computed in a small fraction of a second. Depending on the platform, target frame rates can vary from as low as 30Hz, for a mobile device preserving its battery, to 120Hz and beyond for competitive or virtual reality applications. This means most games have about 10ms to compute each frame.

Processing limitations are of particular interest in games, which are severely constrained in the amount of processing they are able to complete in a single rendered frame. In practice, the physics sub-system in a game may have significantly less than 10ms to work with, since other sub-systems could be competing for the same computational resources. An astrodynamics simulation may have a single millisecond or less in which to make its calculations.

Simulating physics to a high degree of accuracy with an iterative model requires high-resolution time steps. Interactive physics simulations will often run at many times the rendered framerate to maintain stability. For example, simulating an internal combustion engine requires extremely high simulation frequencies to be able to accurately produce sound. To maintain accuracy at a higher rate of passage of time, the simulation frequency has to increase with it. Kerbal Space Program's highest level of time warp is 100,000x normal speed, at which a physics simulation would require computation of 100,000x the time steps per rendered frame to remain stable.

If we instead calculate an object's position from a timestamp, the calculus changes completely. The simulation is no longer constrained by the amount of simulated time the CPU can process per unit real-time. Instead, we are able to jump directly to the time of our choosing, at whatever rate we like, and determine the position of the object afresh every time. The object's position ceases to be dependent on its previous position, and the cost of our calculation becomes unbound from the rate of passage of simulated time, so long as we maintain a constant frame rate. We can even run time backwards - from the simulation's perspective, it does not care a jot.

Planets move in elliptical paths, and ellipses are surprisingly complex. Part of the determination of a planet's position as a function of time is the calculation of the eccentric anomaly from the mean anomaly, which is related by Kepler's equation.

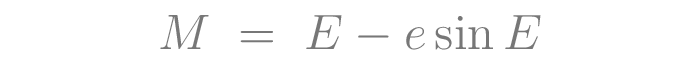
In this equation, E is the eccentric anomaly, the goal of the computation. M is the mean anomaly, which increases linearly over time. The mean anomaly of Earth's orbit increases by pi every six months. e is the eccentricity of the orbit. Having no closed-form solution for E, the equation must be solved with numerical methods. A common choice is Newton-Raphson, a general-purpose root-finding algorithm which converges on successively better approximations through an arbitrary number of iterations. It is straightforward to understand and implement, but it has some major flaws for real-time physics simulation.

For low-eccentricity orbits - those that are nearly circular - Newton-Raphson converges quickly in just a handful of iterations. However, when presented with an eccentric orbit, such as those of the Juno probe, it takes exponentially more iterations to resolve to a high-accuracy solution. With a lower number of iterations, the calculated value for E is erratic and inaccurate, completely unsuitable for a stable simulation.

This presents a massive problem in a real-time system like a game. To be fit for purpose a physics simulation needs to be stable in all reasonable cases the player might encounter, so a Newton-Raphson-based approach would need to be given the resources to run as many iterations as needed to determine a suitably accurate value for E. Since the behaviour is of an exponential increase in computation as orbits become increasingly eccentric, the worst-case performance is many orders of magnitude worse than the best- or even average-case performance. Even if the worst case could be computed accurately while maintaining the target frame rate, in the majority of cases the simulation would use but a fraction of the resources allocated to it. This inefficiency comes at the cost of taking resources away from other sub-systems that could do with it, impacting the quality of the whole application.

There is, thankfully, a solution. While Newton-Raphson is likely to have the best best-case performance - scenarios with nearly-circular orbits - it has appalling worst-case performance. As soft real-time systems, games need to be optimised for the worst-case, such that framerates are consistently high. We also want to make the most of our available resources on every frame, rather than leave most of them unused most of the time. For this, we can turn to that old favourite of computer scientists: a binary search.

Eccentric anomaly determination from Meeus, J. Astronomical Algorithms. Second Edition, Willmann-Bell, Inc. 1991. Translated to pseudo-C from BASIC source.

This approach, while obtuse and archaic, has the property of running in a predictable, constant amount of time, and computes a result to a particular level of precision determined by the number of iterations. On average, it performs worse than Newton-Raphson, taking more runtime to arrive at a result of similar accuracy. However, in the worst-case, it performs just as well in terms of accuracy and runtime as the best-case, which makes it suitable for real-time applications in a way that Newton-Raphson is not. Instead of having to pad the physics budget to account for a worst-case scenario, we can make much more efficient use of a smaller budget, despite the algorithm almost always costing more.

Cheek still smarting, you weigh the ball in your hand. Looking out past the horizon, you think of the ground below your feet. You think through the core of your perfectly spherical virtual planet, and out into the space beyond. You think as far as double-precision floating points can take you - which is, wait, how far?

The distance doesn't really matter anymore, you realise, since the precision is the same for an ellipse a metre across as it is for an astronomical unit. The limit now is double-precision time. Idly bouncing the ball in one hand, you work out what that means. To be accurate to a single frame, you want to be able to represent units of time as short as a frame, or 0.01 seconds. There are about ten million seconds in a year, or billion frames: looking good so far, that's only 10 significant figures, there are a few more to go yet. In a thousand years, the smallest step we can represent is still less than a microsecond, so you keep going. After a million years, the minimum increment finally creeps up to half a millisecond, which sounds about right.

With a grin, you add a healthy number of zeroes, aim, and throw. You watch the ball disappear over the horizon - it does so much more quickly than last time - and turn around to await its return. Sitting down, you look at your watch, start to crank up the passage of time itself. You watch as the ball comes back around... and around, and around, and around again, until it becomes a steady blur over your head, and your mind starts to wander. You start to think about double doubles. You've come a long way, but what's a million years, when you're a planet?

I don't know how Kerbal Space Program computes positions on elliptical orbits - if you do, please get in touch! - but I would be surprised if they used Newton-Raphson. In practice, Kepler's laws are limited in their utility for complex, real-life astrodynamical systems, as they don't take into account tidal effects, irregular gravitational fields, atmospheric drag, solar pressure or general relativity. They also cannot model Lagrange points, which are fundamental to many modern spacecraft such as JWST, or Weak Stability Boundary transfers as used by modern robotic lunar probes such as SLIM. Nonetheless, game developers are a resourceful bunch, so I'm still holding my breath for a game about the Interplanetary Transport Network.